Arduino UNO-t tutvustavas postituses käsitlesime teiste sisendite-väljundite seas ka analoog-digitaalmuundurit. See võtab oma sisendisse tuleva pinge ja pöörab selle mingi suurusega digitaalseks numbriks sõltuvalt sisendpinge ja võrdluspinge suhtest. Mida Arduinol ei ole, on puhtakujuline digitaal-analoogmuundur. DA muundur on seadet mis teeks AD muunduri pöördtehet. See pöörab mikroprotsessoris oleva digitaalarvu vastava suurusega pingeks (või vooluks) oma väljundis.
Väike märkus – ma ütlen puhtakujuline, sest Arduino UNO-l on olemas PWM väljundid mida hoolega filtreerides saab samuti üsna kasutatava DA muunduri. Vaata “https://edb.ee/signaalimuundur/”. See sobib eriti hästi olukordadesse kus süsteem mis DA muunduri sisendit kasutab on aeglase reaktsiooniga ning müra mida kiiresti lülitav digitaalsignaal tekitab ei ole probleem.
Puhtakujuline DA muundur annab aga stabiilse pingenivoo. Kõige lihtsam välja mõeldav DA muundur on üks suur pingejagur.
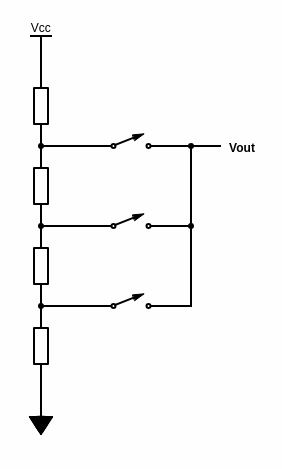
Igal väljavõttel on oma pinge vastavalt sellele kui mitu takistit on temast üleval või allpool. Väga lihtne, aga lülitite ja takistite arv läheb täiesti käest ära kui tahad natukenegi suuremat bittide arvu. Joonisel olev on 2 bitti (4 olekut). Kui tahad 8 bitti tuleb lülitite ja takistite arvuks 254. Lülitid ei ole integraalskeemis mureks, aga takistid võtavad ränil võrdlemisi palju ruumi.
Keerukuselt järgmine oleks teha muundur voolude liitmise teel. Vaata allolevat joonist.
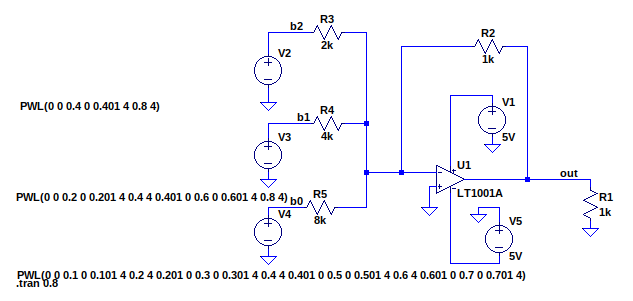
Kui hakkame aktiveerima bitte b0:b2 tekib läbi takistite R3-R5 vool ja see vool kasvatab pinget U1 negatiivsel sisendil. See omakorrda tekitab negatiivse pinge opvõimendi väljundis. Väljundi pinge on selline, et läbi takisti R2 tekib sama suur vool kui on takistite R3-R5 summarne vool.
See DAC on 3 bitiline. Suurima kaaluga bit b2 järel on kaks korda suurem takistus R3 kui tagasisidetakisti R2. Seega peab opvõimendi tekitama kaks korda väiksema väljundpinge kui on meie referentspinge v2. Referentspinge e. võrdluspinge määrab DA muunduri maksimaalse väljundpinge. Samuti määrab võrdluspinge ja DA muunduri bittide arv minimaalse võimaliku muudu suuruse.
Simulatsiooniks valisin referentspingeks 4V. Seega annavad 3 bitilise muunduri 8 võimaliku olekut ühe sammu suuruseks mugavad 0,5V. Simulatsiooni tulemus on näha alloleval pildil. Sammusin kasvavas järjekorras läbi kõik bittide olekud ja graafikult V(out) võib näha väljundi muutumist.
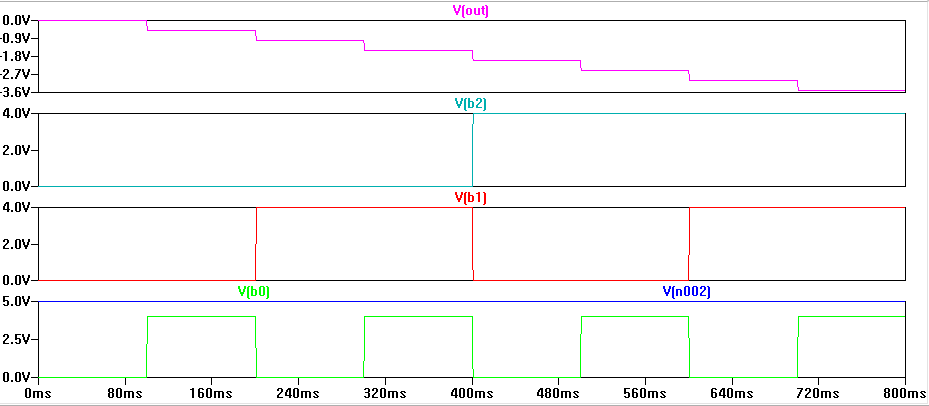
On natuke ebamugav, et see ahel vajab negatiivset pingeallikat. Selle väljundpinge saab taas positiivseks kui kasutame veel ühte opvõimendit inverteeriva võimendina kus võimnendusteguriks on 1.
Horowitz, Hill “The Art Of Electronics” viitab ka asjaolule, et kui tahad rohkem bitte pead kasutama järjest suuremaid takisteid. Suurematel takistitel aga on kalduvus omada suuremat viga mistõttu muutub ka DA muunduri täpsus kehvemaks.
Ja nüüd viimaks DA muundur mille geniaalsus motiveeris mind seda artiklit kirjutama. R-2R redel.
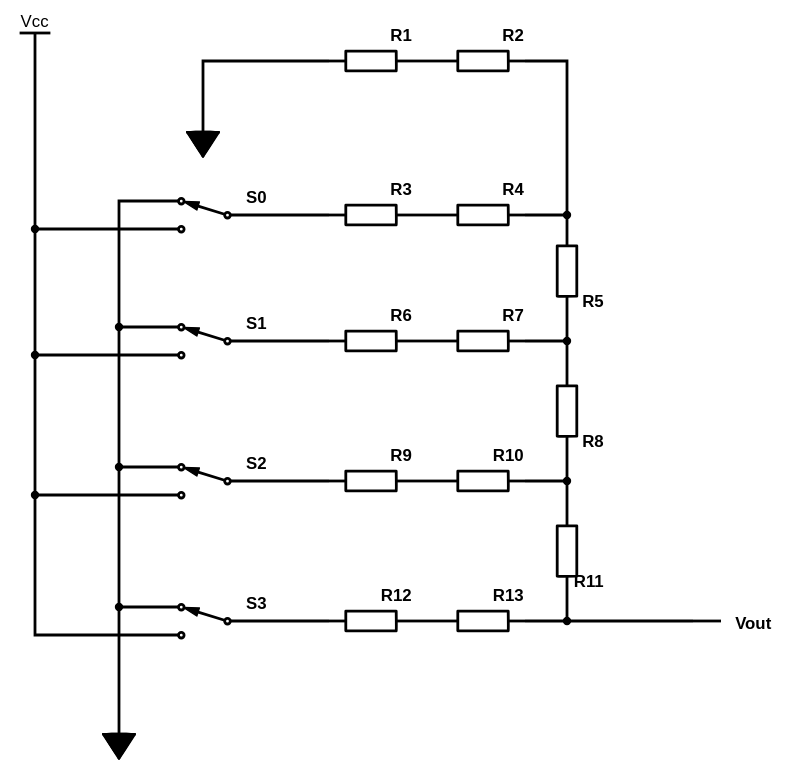
Iga takisti selles reas on ühe ja sama väärtusega R. Kui kõik lülitid on ühendatud maandusega, ning mõõta ahela takistust punktist Vout saab takistuseks ühe takisti nominaali R. Ühendada Vout maandusega, ning mõõta Vout voolu, siis sulavlise lüliti kombinatsiooni korral on vool üks ja seesama. Ehk siis igas olukorras on selle ahela väljundtakistus R.
Selle skeemi lahtimõtlemine oli esimene kord pärast ülikooli kui kasutasin Thevenini teoreemi.
Üritasin tuvastada kes selle ahela leiutas. Wikipedia märgib esmamainimisena artiklit ajakirja “A Journal of Communications and Electronics Engineering” 1953 aasta augustinumbris. Selles ajakirjas aga käsitletakse R-2R redelit kui kõigile tuttavat ja iseenesest mõistetavat ahelta. Seega jääb kahjuks leiuta hetkel teadmata.
Tuues teema ringiga tagasi Arduino juurde – Lülitid S0-S3 võivad olla Arduino UNO või suvalise mikrokontrolleri digitaalväljundid. Seega on siin viis kuidas odava mikrokontrolleri külge elementaarne DAC tekitada.
Et asi ei jääks vaid teoreetiliseks ostsin peotäie 1kΩ takisteid ja ehitasin ühe R-2R redeli.

Paigaldasin paar lülitit redeli bittide lülitamiseks 0V ja 10V vahel ja mõned kiirühenduse pesad. Toitepinge 10V teeb igasugused arvutused lihtsaks.

Süsteemi kontrolliks klõbistasin läbi kõik 16 võimaliku lülitikombinatsiooni ning mõõtsin multimeetriga iga kombinatsiooni väljundpinge ja -voolu
|
Bit-i number |
Binaarväärtus |
Teoreetiline pinge [V] |
Mõõdetud pinge [V] |
Mõõdetud vool [mA] |
Arvutatud takistus [Ω] |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0.625 |
0.61 |
0.6 |
1016.667 |
|
2 |
10 |
1.25 |
1.23 |
1.2 |
1025 |
|
3 |
11 |
1.875 |
1.84 |
1.81 |
1016.575 |
|
4 |
100 |
2.5 |
2.47 |
2.41 |
1024.896 |
|
5 |
101 |
3.125 |
3.06 |
2.99 |
1023.411 |
|
6 |
110 |
3.75 |
3.69 |
3.61 |
1022.161 |
|
7 |
111 |
4.375 |
4.3 |
4.23 |
1016.548 |
|
8 |
1000 |
5 |
4.95 |
4.83 |
1024.845 |
|
9 |
1001 |
5.625 |
5.53 |
5.44 |
1016.544 |
|
10 |
1010 |
6.25 |
6.16 |
6.04 |
1019.868 |
|
11 |
1011 |
6.875 |
6.75 |
6.67 |
1011.994 |
|
12 |
1100 |
7.5 |
7.42 |
7.22 |
1027.701 |
|
13 |
1101 |
8.125 |
8 |
7.88 |
1015.228 |
|
14 |
1110 |
8.75 |
8.65 |
8.51 |
1016.451 |
|
15 |
1111 |
9.375 |
9.27 |
9.14 |
1014.223 |
Mõõdetud voolust ja pingest arvutasin mis on R-2R ahela takistus iga kombinatsiooni korral. Mõningane ebatäpsus tõesti, kuid põhimõtteliselt ikkagi 1kΩ. Panin teoreetilise ja mõõdetud väljundpinge ühele graafikule.
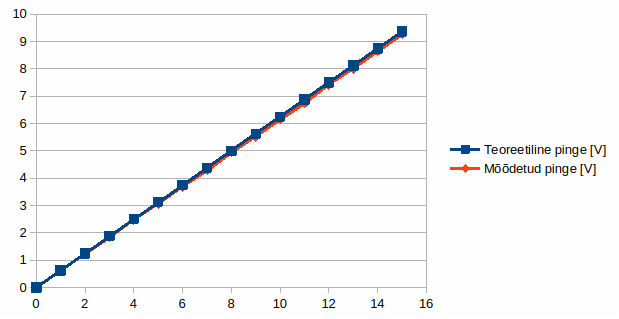
“Kõik geniaalne on oma olemuselt lihtne” ütles üks TTÜ reklaam kunagi. Ja R-2R ahel on geniaalne.
